O gravitačním a tíhovém poli - díl čtvrtý
Otázka homogenity zemského gravitačního pole:
Gravitační pole Země není ve skutečnosti homogenní a dokonce ani centrální, neboť Země není kulatá a také není homogenní (hustota Země je proměnná v závislosti na poloze). Otázka zní, za jakých podmínek můžeme nehomogenitu pole zanedbat. Na tuto otázku lze odpovědět, jestliže nejprve zadáme přesnost určení intenzity pole. Požadujeme-li např. přesnost s relativní chybou menší než 0.001, pak vzdálenost od středu Země se může měnit směrem od středu jen o 0.0005 R, tedy asi o 3 km. Chceme-li zanedbat rozdíly ve směru do 1°, musíme se omezit na plochu o poloměru cca 56 km se středem v daném stanovišti. Přitom ovšem neuvažujeme nerovnosti povrchu (hory) a změny hustoty.
Gravitační pole množiny hmotných bodů
Je-li gravitační pole vytvářeno větším počtem hmotných bodů (nebo těles), je intenzita v daném místě pole vektorovým součtem intenzit jednotlivých polí a potenciál pole je součtem potenciálů v jednotlivých polích.
Silové pole na povrchu rotující koule:
Na těleso nalézající se na povrchu homogenní rotující koule (např. kulovém modelu Země) působí kromě gravitační síly také síla setrvačná (v některé literatuře nazývaná silou odstředivou), ovšem posuzujeme-li kouli v soustavě s ní pevně spojené (tj. s ní rotující). Velikost této síly je dána vztahem
Fs = mω2ξ,
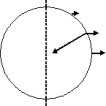
Výsledná síla je vektor FG se složkami (v dvojrozměrné pravoúhlé souřadné soustavě)o velikostech Fgcosφ - Fs a Fgsinφ. Velikost tohoto vektoru je
Fg = √[(FgcosΦ-Fs)2+(FgsinΦ)2].
Tíhová síla ovšem nesměřuje do středu koule.
Podíl tíhové síly a hmotnosti tělesa, na které tato síla působí, je intenzita tíhového pole totožná s tíhovým zrychlením g. Tíhové pole je tedy pole popsatelné tíhovým zrychlením.
Příklad: Podíl setrvačné síly a hmotnosti tělesa na rovníku Země (která je ovšem rotujícím nepravidelným tělesem, nikoliv koulí) je daný výrazem ω2R = 0.03392 m/s2, kde ω je úhlová rychlost rotace Země vůči hvězdám. Velikost gravitačního zrychlení (tj. intenzity gravitačního pole) na povrchu Země může být snížena nejvýše o tuto hodnotu. Jen na pólech Země se tíhové a gravitační zrychlení rovnají. Značkou tíhového zrychlení je g. Na pólech je g = 9.832 m/s2, na rovníku g = 9.8109 m/s2, normální tíhové zrychlení je gn = 9.80665 m/s2.
Reference:
[1] Internet, www.wikipedia.org
[2] Kleczek J., Švestka Z., Astronomický a astronautický slovník (Orbis, Praha 1963)
[3] Železný V., Návraty první dámy (Panorama, Praha, 1986)
Seriál
- O gravitačním a tíhovém poli - díl první
- O gravitačním a tíhovém poli - díl druhý
- O gravitačním a tíhovém poli - díl třetí
- O gravitačním a tíhovém poli - díl čtvrtý
- Definování polohy kosmického tělesa - díl první
- Definování polohy kosmického tělesa - díl druhý
O autorovi
Miroslav Šulc
Narozen 1941, v roce 1963 promoval na přírodovědecké fakultě Univerzity J. E. Purkyně (dříve a nyní Masarykova univerzita) v oboru matematika-fyzika (s titulem promovaný fyzik-učitel). Od té doby zaměstnán jako učitel na střední škole. Od r. 1954 do r. 1986 externí spolupracovník brněnské hvězdárny. Od r. 1959 člen České astronomické společnosti. Od r. 1996 hospodář výboru SMPH. Od r. 2006 v definitivním důchodu.
