Teleskopie - díl osmý (Použití dynametru v astronomické optice)
Astronom-amatér se však střetává při svých aktivitách v oblasti astronomických přístrojů s případy, kdy potřebné údaje chybí, a proto hledá jednoduché metody, jak je zjistit. Je to velmi aktuální problém nejen tehdy, když chce použít určitý spojný systém ve funkci okuláru. S touto situací se velmi často setkáváme, jelikož astronomické okuláry jsou drahé a amatéři si mohou občas vypomoci různými náhradami. V následujících řádcích si zrekapitulujeme dva snadno zjistitelné parametry dalekohledu. Ty můžete využít nejen pro určení zvětšení, ale i dalších charakteristik teleskopu. Uvedenými parametry jsou vstupní a výstupní pupila dalekohledu.
Vstupní pupila
Vstupní pupila (označovaná D) je u správně konstruovaného dalekohledu dána přední plochou jeho objektivu na okrajích ohraničenou jeho objímkou. Přesněji bývá definována jako clona s otvorem nejmenšího průměru před čočkami dalekohledu nebo obraz otvoru některé clony uvnitř přístroje, který by byl menší než obraz všech ostatních clon, a to při pozorování z bodu na osovém paprsku v nekonečnu.
Součástí dalekohledu je vždy několik clon. Můžeme je jednoduše popsat jako plochy s kruhovými otvory, kterými procházejí světelné paprsky v tubusu dalekohledu. Patří k nim však i objímky objektivu a případně i další optické části. Často je kruhová clona umístěna i před objektivem, jako ochrana proti rozptýlenému světlu a rose. Když se podíváme na tyto clony z bodu, který se nachází ve větší vzdálenosti na prodloužené ose dalekohledu, vidíme jejich otvory pod zornými úhly. Clona, kterou vidíme pod nejmenším úhlem (tedy otvor vidíme jako nejmenší) je vstupní pupilou. Clona, která ji tvoří je otvorová clona (nebo také clona světelnosti). Je třeba poznamenat, že clony umístěné za objektivem v tubusu mají postupně se zmenšující průměr otvoru, který je vždy menší než průměr objímky objektivu.
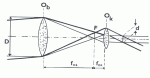
Z místa pozorovaného předmětu však vidíme jejich obraz, který je zvětšený spojným systémem objektivu, proto vidíme jejich zdánlivý průměr větší než je průměr objektivu. Clony v tubusu dalekohledu umístěné mezi objektivem a okulárem mají za úkol odstranit rozptýlené světlo odražené od stěn tubusu. To by znehodnotilo získaný obraz. Průměry jejich otvorů musí být zvolené tak, aby neblokovali okrajové paprsky, přicházející od objektivu. V případě, že by k tomu došlo, přebírala by (podle výše uvedené definice) taková clona s příliš malým otvorem úlohu vstupní pupily.
Průměr vstupní pupily D měříme pravítkem nebo přesněji posuvným měřítkem.
Výstupní pupila
Výstupní pupila dalekohledu (označovaná d) vzniká jako obraz vstupní pupily za okulárem přístroje. Když se podíváme na okulár dalekohledu namířeného na oblohu nebo na jinou světlou plochu, uvidíme uprostřed oční čočky okuláru světlé kruhové pole, zatímco zbytek oční čočky je zřetelně tmavší.
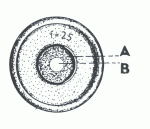
Vstupní i výstupní pupila je vytvářena právě tou clonou, kterou je u Keplerova dalekohledu (se spojnou soustavou ve funkci okuláru) okraj objímky objektivu na jeho vnější ploše. Můžeme se o tom přesvědčit i tak, že při pozorování výstupní pupily lupou uvidíme obraz každého průmětu, který položíme na venkovní plochu objektivu, což má i svoje využití při zjišťování některých charakteristik dalekohledu.
V případě výstupní pupily nás zajímá její průměr s její vzdáleností od oční čočky okuláru (za přístrojem).
Průměr výstupní pupily je ve většině případů malý (od zlomku milimetrů po 10 mm). Naší snahou je zjistit tento údaj s dostatečnou přesností (0,1 mm). Protože přímé měření pupily přiložením měřidla s milimetrovým dělením by nám dávalo jen přibližné výsledky, použijeme k tomuto účelu tzv. Ramsdenův dynametr. Jesse Ramsden (1735-1800) ho zkonstruoval před více než dvěmi sty lety, ale ani v současné době neztratil svůj praktický význam.
Podstatnou částí dynametru je měřidlo, dělené na desetiny milimetrů s celkovou délkou přibližně 10 mm. Jeho neprůhledné dílky jsou naznačeny na průhledné destičce kruhového tvaru, vyrobené ze skla, nebo z plastu. Tuto stupnici pozorujeme lupou, což nám dovoluje po přiložení dynametru k okuláru měřit průměr výstupní pupily.
Skleněná kruhová destička se stupnicí vhodného druhu se nachází v tzv. mikrometrických okulárech, používaných v mikroskopech na měření mikroskopických objektů. Jsou to většinou okuláry Huygensova typu s mikrometrickou destičkou mezi čočkami, takže takový okulár se pro přímé použití ve funkci Ramsdenova dynametru nehodí. Místo něj můžeme použít jen vlastní destičku se stupnicí, kterou je možné z okuláru vyndat.
Jinou možnost poskytuje zhotovení potřebné stupnice fotografickou cestou. Na málo citlivý černobílý kinofilm nafotografujeme okraj průhledného měřidla (pravítka z průhledného plastu) a to část 10 cm dlouhou (0-10 cm = 100 mm). Fotoaparát přitom umístíme ve vzdálenosti (a) od měřidla, která se bude rovnat 11ti násobku ohniskové vzdálenosti objektivu fotoaparátu (f).
a = 11 x f
V případě přístroje na kinofilm je u běžných objektivů f = 50 mm budeme tedy obraz pravítka snímat ze vzdálenosti 11 x 50 mm = 550 mm. Tuto vzdálenost odměříme ne od okraje objektivu, ale alespoň přibližně od středu mezi vnějšími plochami přední a zadní čočky. Pro tento účel je vhodný fotoaparát tzv. jednooká zrcadlovka na kinofilm, který dovoluje zaostřit obraz objektu na malé vzdálenosti. V našem případě (při f = 50 mm) stačí nastavit zaostření podle stupnice vzdálenosti na 55 cm a potom se přiblížit s fotoaparátem tak, abychom pravítko viděli v hledáčku docela ostře. Použijeme clonu 1:11 až 1:18. Pravítko musíme položit na bílou plochu a dobře ho osvětlit tak, aby se netvořili stíny. Plocha pravítka by neměla být porušena, jelikož rýhy a jiné poškození bude viditelné i na hotovém měřidle. Vyrobíme několik snímků při různých expozicích. Na kinofilmu získáme zmenšený negativní obraz v poměru 1:1, takže toto měřidlo bude dlouhé 10 mm a rozdělené na 100 dílků. Negativ okopírujeme na kousek stejného filmu. V tmavé místnosti položíme negativ na kousek filmu citlivými vrstvami k sobě tak, aby se negativ nacházel na vrchní straně a zakryjeme ho skleněnou destičkou. Potom negativ osvětlíme žárovkou a obraz překopírujeme. Po vyvolání dostaneme pozitivní obraz měřidla (černé dílky na průhledném podkladě). Ze získaného pozitivu opatrně vystřihneme kruhovou plošku s měřidlem, kterou potom umístíme do malé objímky a s ní do trubičky dynametru. Jelikož filmový materiál má tendenci se přehýbat, musíme naše měřidlo přitlačit do objímky po obvodě prstencovitou vložkou.
Pokud byste se uspokojili s menší přesností měřidla, můžeme do dynametru namontovat kousek průhledného pravítka nebo si vyznačit milimetrovou stupnici na kousku průhledné fólie (např. z rentgenového filmu po umytí emulzí), kterou potom vystřihneme do potřebného tvaru. V tomto případě bude přesnost měřidla (odhadem) na hranici 1/5 mm.
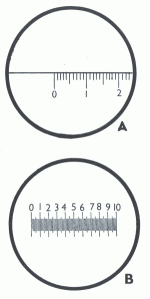
Pohodlné a přesné měření výstupní pupily nám umožní dynametr, zkonstruovaný jako slabě zvětšující mikroskop s mikrometrickým okulárem, o kterém jsme se již zmínili. Hodnotu dílků mikrometru si však musíme otestovat pozorováním vhodného měřidla, které bude položené před mikroskopem. Pokud máme k dispozici potřebný mikrometrický okulár, jako objektiv mikroskopu, můžeme použít achromatickou spojnou čočku s ohniskovou vzdáleností 20 až 30 mm nebo mikroskopický objektiv se zvětšením 3x až 4x. Vzdálenost mezi objektivem a okulárem volíme 120 až 160 mm (s délkou mikroskopu narůstá jeho zvětšení).
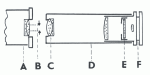
Pro zájemce, kteří by si chtěli zkonstruovat Ramsdenův dynametr nebo se pokusit alespoň o jeho improvizaci, přinášíme následující návrh.
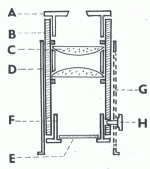
Dynametr se skládá z několika trubic různých délek s průměrem přibližně 24-30 mm (podle průměru použité optiky), které jsou zasunuty do sebe a umožňují (s určitým odporem) vzájemný pohyb.
První trubička obsahuje dvojčočkovou lupu např. Wilsonova typu se 6 až 8 násobným zvětšením. Do části této trubičky, obrácené k oku je zasunuta miskovitá část s clonou o průměru 5 až 8 mm, která zajišťuje, aby do oka vstupovaly jenom paprsky procházející středem dynametru, což umožní přesné odečítání průměru výstupní pupily. Vzdálenost clony od lupy je možné regulovat posunem misky v trubičce dynametru. Po zjištění vhodné vzdálenosti misku s clonou přilepíme nebo zajistíme šroubkem.

Druhá krátká trubička v podobě misky je na předním okraji zúžená. Zde se opírá mikrometrické měřidlo, které v objímce upevníme prstencem z kovu nebo z plastu. Vzájemný posun trubičky s měřidlem v trubičce s lupou je potřebný na to, abychom našli vhodnou vzdálenost měřidla od lupy, při které budeme vidět jeho stupnici dobře zaostřenou. V této poloze je potom potřebné trubičku s měřidlem upevnit (šroubkem nebo přilepením), aby se zaostření neporušilo.
Poslední trubička, která je volně nasunutá na trubičku s lupou, slouží jako opora při měření pupily. Zabezpečuje správnou polohu dynametru, tedy souběžnou s osou dalekohledu a současně stínící boční světlo, které ruší (někdy až znemožňuje) vlastní měření. Tuto trubičku opřeme o vnější plochu okuláru, přičemž trubička s lupou je do ní zasunuta tak, aby stupnice měřidla byla co nejblíže u oční čočky okuláru. Potom vytahujeme trubičku s lupou a s měřidlem směrem od oční čočky a díváme se při tom do dynametru. Když uvidíme výstupní pupilu jako kruhovou plošku s ostrým okrajem, je zaostření dokonalé a můžeme zjistit průměr pupily podle počtu dílků měřidla, které pokrývá. Měřidlo vidíme ostře spolu s obrazem výstupní pupily. V trubičce, která spojuje dynametr s měřícím okulárem, je vypracována podélná štěrbina, kterou předjíždí šroubek, závitem přichycený k tělesu dynametru. Umožňuje vzájemné upevnění těchto dvou částí v potřebné poloze.
Pokud chceme měřit vzdálenost výstupní pupily od oční čočky, můžeme si na venkovní plochu trubičky s měřidlem naznačit milimetrovou stupnici, která bude udávat, jaká je vzdálenost měřidla od oční čočky (tedy od konce opěrné trubičky). Při zaostřeném obrazu výstupní pupily se její rovina totiž nachází v rovině měřidla. Pokud je oční čočka okuláru měřeného dalekohledu zapuštěna hlouběji pod úroveň vnější plochy okuláru, musíme si tuto vzdálenost změřit a připočítat k údajům stupnice na dynametru.
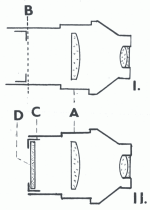
Pokud máme k dispozici ortoskopický okulár (např. mikroskopický okulár Meopta O 10x) nebo jiný typ okuláru s clonkou před optickou soustavou, můžeme po malé úpravě získat podstatnou část dynametru (lupu s možností umístění měřidla), kterou doplníme jen opěrnou trubičkou pro přiložení k okuláru dalekohledu. Tato úprava spočívá v tom, že z předního konce okuláru vybereme plechovou clonu zorného pole a zkrátíme jeho tubus asi o 7 mm oddělením jeho přední části. Potom vložíme do clony měřidlo a upevníme ho vhodným prstencem. Dále nasadíme clonu zpět do tubusu okuláru tak, aby její kruhovitý otvor směřoval ven. Tak bude možné měřidlo v cloně přiblížit co nejvíce k oční čočce. Opatrným zatlačením clonky s měřidlem do tubusu okuláru ji posuneme do takové polohy, ve které budeme vidět jeho obraz v tomto improvizovaném dynametru zaostřený. Na upravený okulár potom nasuneme trubičku pro spojení s okulárem měřeného dalekohledu. Jelikož na okuláru, upraveném na dynametr máme možnost zachytit jen trubičku malé délky, která nám dovolí sledovat výstupní pupilu, jen pokud se nachází blízko oční čočky, pro měření výstupní pupily ve větší vzdálenosti si připravíme jinou delší trubičku.
Ortoskopický okulár (bez opěrné trubičky) můžeme i nadále používat jako okulár v dalekohledu, případně i s naším měřidlem. Po zjištění úhlové hodnoty jeho dílků (např. změřením průměru úplňku Měsíce) můžeme tento jednoduchý mikrometr používat i na měření malých úhlových vzdáleností na obloze.
Uveďme si několik příkladů použití dynametru při měření parametrů astronomických dalekohledů.
1. průměr výstupní pupily
Světlo, které vstoupí do objektivu dalekohledu se soustředí do plochy výstupní pupily a vstupuje přes ni do našeho oka. Pokud by byl průměr výstupní pupily větší než průměr zornice oka (oční pupily), potom by se část světla získaná objektivem nedostávala do oka, ale bez užitku by se ztratila. Proto bývá průměr výstupní pupily dalekohledu menší než průměr oční pupily, nebo se rovná jejímu průměru. Zornice oka mění svůj průměr s osvětlením. Ve tmě se rozšiřuje na maximum, které dosahuje podle věku od 8 mm (u dvacetiletých) až po 2,8 mm (u osmdesátiletých). Shodu průměrů výstupní pupily s pupilou mladého oka (7 mm) dosáhneme při tzv. normálním zvětšení Zn, které je určeno podílem průměrů objektivu v milimetrech Dmm a maximálního průměru zornic (7 mm),
Zn = Dmm / 7.
Normální zvětšení je vhodné v astronomických dalekohledech používat při pozorování plošných objektů (mlhovin, komet) a tam, kde potřebujeme mít k dispozici velké zorné pole.
Dalekohled nám svým objektivem soustředí do oka tolikrát více světla, kolikrát je plocha objektivu větší než plocha oční zornice při jejím rozšíření na maximum. Pokud neuvažujeme o ztrátách odrazem a absorpcí v optice přístroje, světlost dalekohledu bychom mohli vyjádřit jako poměr plochy objektivu D2 a zornice d2.
S = D2 / d2.
2. poloha výstupní pupily
Poloha výstupní pupily je dána její vzdáleností od oční čočky okuláru dalekohledu. Můžeme ji zjistit vhodně upraveným dynametrem, jak již bylo uvedeno. S výjimkou speciálních případů je vzdálenost výstupní pupily úměrná ohniskové vzdálenosti okuláru, a tedy klesá s rostoucím zvětšením dalekohledu. Poznat polohu výstupní pupily je důležité, jelikož do tohoto místa musíme dostat zornici oka, pokud chceme dosáhnou optimálních podmínek pro pozorování dalekohledem. Při větší vzdálenosti výstupní pupily od oční čočky okuláru umisťujeme do její roviny vhodnou clonu, která má podobu misky, připojené na okulár za oční čočkou s otvorem vhodného průměru. Okuláry s větší vzdáleností výstupní pupily jsou výhodné pro ty, kteří nosí brýle, hlavně v případech, kdy jde o astigmatizmus oka, protože v těchto případech je nutné použít při pozorování dalekohledem vhodné brýle.
3. zvětšení dalekohledu
Zvětšení dalekohledu je možné zjistit jako poměr průměru vstupní pupily D a výstupní pupily d.
Zz = D / d.
I když způsobů určení zvětšení dalekohledu je několik, metoda vycházející z porovnání obou pupil je určitě nejjednodušší.
4. ohnisková vzdálenost okulárů
Ohniskovou vzdálenost okulárů fok si můžeme zjistit podle níže uvedeného vzorce, tak poznáme zvětšení dalekohledu a ohniskovou vzdálenost jeho objektivu. Zvětšení si určíme metodou uvedenou v bodě 1 (zvětšení dalekohledu). Máme k dispozici okulár, jehož ohniskovou vzdálenost známe, potřebnou ohniskovou vzdálenost objektivu si lze odvodit podle vzorce
fok = fob / Z.
V případě potřeby můžeme použít i jiné jednoduché metody měření ohniskových vzdáleností objektivu, např. promítnutí obrazu Slunce či Měsíce a změření promítací plochy od zadané plochy objektivu při zaostřeném obrazu. Můžeme vycházet také z měření promítnutého obrazu Měsíce nebo Slunce, který dostaneme v ohnisku objektivu (M) a ohniskovou vzdálenost potom vypočítáme podle vzorce
fob = 113,6 x Mmm
Použití dynametru na určení ohniskové vzdálenosti okuláru bude asi nejčastějším způsobem jeho využití, jelikož určit tuto charakteristiku jeho vícečočkové soustavy jinou metodou není snadné. Pokud je předpoklad řešit tuto úlohu častěji, vyplatí se ve vhodné trubici instalovat objektiv (stačí i okulárová čočka o mohutnosti přibližně +3 dioptrie) se známou ohniskovou vzdáleností a se známým průměrem. Do tohoto dalekohledu potom upevníme okulár, který chceme měřit, zaostříme si v jeho zorném poli vzdálený objekt, změříme dynametrem průměr výstupní pupily a po dosazení potřebných údajů do vzorce zjistíme hledanou fok.
5. průměr objektivu
Průměr objektivu nebo vstupní pupily (přesněji efektivní vstupní pupily) si můžeme ověřit v případě, že chceme zjistit, jestli clony v dalekohledu, které zabraňují rozptylu světla na stěnách tubusu, mají správnou velikost otvorů a neblokují vstup okrajových paprsků z objektivu do okuláru. V případě, že je otvor některé z těchto clon příliš malý, nemůže se uplatnit všechno světlo, které objektiv přijal, takže pracujeme vlastně s dalekohledem, jehož objektiv má menší průměr, než jaký jsme zjistili změřením průměru přední plochy objektivu (tedy předpokládané vstupní pupily). Velikost (efektivní) vstupní pupily potom určuje tato clona, která má nevhodný, příliš malý průměr.
Taková situace může vzniknout při amatérské konstrukci dalekohledu a má za následek snížení rozlišovací schopnosti, snížení zisku na magnitudách pozorovaných hvězd, apod. Proto se snažíme vyhnout se těmto chybám a případně je po zjištění odstranit.
Na druhé straně je třeba upozornit, že podle zpráv z odborných časopisů se zjistilo, že u některých astronomických dalekohledů byla vstupní pupila úmyslně zmenšena clonou v tubuse, takže efektivní vstupní pupila neodpovídala průměru objektivu v objímce (t. j. předpokládané vstupní pupile). Cílem takovéto úpravy je tlumit optické nedostatky objektivu nižší kvality, které jsou při zmenšení jeho účinného průměru dosti výrazné.
Skutečný průměr vstupní pupily (efektivní průměr objektivu) De zjistíme jako násobek zvětšení Z a průměru výstupní pupily d
De = Z x d.
Pro tento výpočet si však musíme nejprve vypočítat přesné zvětšení přístroje podle vzorce (v části 3. Zvětšení dalekohledu). Abychom vyloučili chybu vyplývající z nejistého průměru efektivní vstupní pupily, pokryjeme objektiv dalekohledu maskou se čtvercovým otvorem. Úhlopříčka tohoto otvoru bude o 15 až 20 mm menší než průměr objektivu. Výstupní pupila bude také čtvercová, takže obě bude možno přesně změřit a zjistit tak zvětšení. Po odstranění čtvercové clony uskutečníme znovu měření výstupní pupily d. Dosadíme ho spolu s předem zjištěným zvětšením do výše uvedeného vzorce a vypočítáme De (průměr efektivní vstupní pupily). Pokud je De stejné jako průměr přední plochy objektivu v objímce, je clonový systém v pořádku a světelnost dalekohledu je neporušená. Pokud je vypočítaný De menší než průměr objektivu (D), má některá clona v tubuse příliš malý otvor a snižuje efektivnost objektivu.
6. ohnisková vzdálenost objektivu
Ohniskovou vzdálenost objektivu zjistíme podle vzorce
fob = Z x fok,
přičemž zvětšení Z určíme podle vstupní pupily D a výstupní pupily d (podle vzorce v části 3. Zvětšení dalekohledu). Použijeme přitom okulár známé ohniskové vzdálenosti fok. Tato metoda je užitečná v případech, kdy pouzdro přístroje znemožňuje jiný způsob měření fob, například při hranolových systémech vestavěných do dalekohledu. V některých případech je objektiv vícečlenný a představuje delší optickou soustavu, takže měření ohniskové vzdálenosti od zadané optické plochy je velmi nepřesné. Tak je tomu např. v dlouhoohniskových fotoobjektivech, které v případě potřeby provizorně uložíme do vhodné trubice a připojíme okulár se známou fok. Tento improvizovaný dalekohled potom zaostříme na vzdálený předmět, určíme zvětšení a potom vypočítáme hledanou fob.
V případě, že potřebuje takto posoudit fotoobjektiv s kratším ohniskem, umístíme ho do dalekohledu jako okulár a jeho f určíme podle vzorce (v části 4. Ohnisková vzdálenost okulárů).
Původní článek byl publikován v Astronomické ročenke (SK) v roce 2003.
Úprava: Petra Váňová
Teleskopie: Nový seriál Jihlavské astronomické společnosti poskytuje cenné rady o konstrukcích astronomických přístrojů v amatérských podmínkách. Autorem seriálu je doc. RNDr. Ivo Zajonc, CSc., autor mnoha publikací nejen o astronomické technice.
Články ze seriálu TELESKOPIE byly v minulých letech postupně uveřejňovány v Astronomické ročenke vydávané Slovenskou ústrednou hvezdárňou v Hurbanove - http://www.suh.sk. Děkujeme vedení tohoto ústavu za souhlas se zveřejněním těchto aktualizovaných příspěvků na webu Jihlavské astronomické společnosti - jiast.cz a České astronomické společnosti - astro.cz.

Seriál
- Teleskopie – díl první (Jaký dalekohled je vhodný pro astronoma amatéra?)
- Teleskopie – díl druhý (Zkoušení optického systému astronomických dalekohledů)
- Teleskopie – díl třetí (Jednoduché metody měření a výpočty pro amatérskou konstrukci dalekohledů)
- Teleskopie – díl čtvrtý (Jednoduchý astronomický dalekohled)
- Teleskopie – díl pátý (Triedr v astronomii)
- Teleskopie – díl šestý (Okuláry pro amatérské dalekohledy)
- Teleskopie – díl sedmý (Centrování dalekohledů a nastavení paralaktických montáží)
- Teleskopie - díl osmý (Použití dynametru v astronomické optice)
- Teleskopie - díl devátý (Okno jako astronomická pozorovatelna )
- Teleskopie - díl desátý (Astronom amatér a jeho zrak)
- Teleskopie - díl jedenáctý (Pomůcky pro přímé pozorování Slunce)
- Teleskopie - díl dvanáctý (Projekční metoda pozorování Slunce)
- Teleskopie - díl třináctý (Protuberanční nástavec pro amatérské dalekohledy)
- Teleskopie - díl čtrnáctý (Jednoduché zařízení pro astrografii)
- Teleskopie - díl patnáctý (Fotografujeme astronomickým dalekohledem)
- Teleskopie - díl šestnáctý (Amatérský helioskop)
- Teleskopie - díl sedmnáctý (Prodloužení a zkrácení ohniskové vzdálenosti objektivu - Barlowova a Shapleyova čočka)
- Teleskopie - díl osmnáctý (Optické filtry při amatérských astronomických pozorováních)
- Teleskopie - díl devatenáctý (Jednoduchý způsob měření úhlových vzdáleností na obloze)