Jak funguje astronomický dalekohled - díl první

Zmíněné dotazy jsou ovšem důvodné, protože většina lidí vlastnících dalekohled jej používá k pozemním pozorováním, u nichž zvětšení dalekohledu a tudíž zvětšení zdánlivých zorných úhlů pozorovaných předmětů je základním jevem, který dává použití dalekohledu smysl.
Uveďme nejdříve zcela základní informace o astronomických dalekohledech. Dělí se do dvou skupin:
- refraktory, využívajících k zobrazení předmětu lomu světla;
- reflektory, využívajících k zobrazení předmětu (kromě lomu světla) odrazu světla.
Každý z uvedených typů obsahuje alespoň dva optické členy:
- objektiv, vytvářející obraz pozorovaného předmětu;
- okulár, sloužící k pozorování obrazu, vytvořeného objektivem.
Konstrukční rozdíl mezi refraktorem a reflektorem spočívá v tom, že objektivem refraktoru je spojná čočka (v principu; ve skutečnosti kombinace spojek), kdežto objektivem reflektoru je duté zrcadlo (obvykle ve tvaru rotačního paraboloidu; tento tvar je laikovi znám, neboť je užit u satelitních televizních antén).
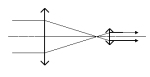
- dalekohled holandský (nazývaného také Galileiho; nesprávně Galileův), jehož okulárem je rozptylná čočka ("zmenšující" rozptylka, která je známá jako brýlová čočka krátkozrakých osob). Ten je znám jako "divadelní kukátko". V astronomii už používaný není.
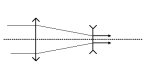
- dalekohled Keplerův, jehož okulárem je spojka (v principu; ve skutečnosti kombinace dvou spojek), zastávající zde funkci lupy. Tento typ dalekohledu je v běžném použití znám jako triedr, jenž však obsahuje další optické prvky, totiž dva pravoúhlé optické hranolky v každé ze dvou optických cest; které způsobují převrácení převráceného obrazu, takže při pozorování vidíme"normálně".
Sestava obou typů dalekohledu je v podstatě stejná. Při pozorování předmětu "v nekonečnu" je obraz předmětu vytvořen objektivem v rovině jeho obrazového ohniska, které splývá s předmětovým ohniskem okuláru, jenž funguje jako lupa; čočka oka pak vytvoří skutečný obraz sítnici. Rozdíl mezi oběma typy dalekohledů spočívá v tom, že předmětové ohnisko okuláru Keplerova dalekohledu se nalézá v předmětovém prostoru okuláru (spojky), kdežto u holandského dalekohledu se předmětové ohnisko okuláru (rozptylky) nalézá v jeho obrazovém prostoru. U holandského dalekohledu se tedy paprsky vycházející z objektivu nemohou vytvořit skutečný obraz, protože mezi objektivem a jeho obrazovým ohniskem je umístěna rozptylka, která přemění sbíhavý svazek paprsků na svazek rovnoběžných paprsků. Jinak řečeno: skutečný obraz, který by byl vytvořený objektivem (nebýt rozptylky) se stává pro rozptylku zdánlivým předmětem, který rozptylka přemění na skutečný obraz, ležící ale v nekonečnu; čočka oka opět vytvoří skutečný obraz na sítnici. (Rozptylka obecně vytváří zdánlivé obrazy skutečných předmětů, ale může také vytvořit skutečné obrazy zdánlivých předmětů. Viz poznámka 1.)


Lze odvodit, že absolutní hodnota úhlového zvětšení obou typů dalekohledů (při pozorování předmětů s nepatrným zorným úhlem) je dána poměrem absolutních hodnot ohniskových vzdáleností objektivu a okuláru (v tomto pořadí). Jestliže např. ohnisková vzdálenost objektivu bude 200 cm a ohnisková vzdálenost okuláru (v abs. hodnotě) 1 cm, dosáhneme tak dvěstěnásobného zvětšení. (Vztah pro zvětšení platí i pro reflektory, jimiž se zde ale nebudeme zabývat, neboť níže uvedené skutečnosti platí i pro ně.)
Praktický rozdíl mezi holandským a Keplerovým dalekohledem je ten, že v holandském vidíme předměty "přímé", kdežto v Keplerově "převrácené". Galilei používal dalekohledu holandského, v astronomii se používá již několik století dalekohled Keplerův.
Na počátku byly zmíněny dvě otázky návštěvníků. Odpovíme nejprve na druhou. Hvězdy nemůžeme v dalekohledu vidět jako plošné objekty, neboť jsou příliš vzdálené. Např. hvězda o průměru 10 mil. km (Slunce má průměr cca 1,4 mil. km) ve vzdálenosti 10 světelných let t.j. 9,467.1015 km se jeví pouhým okem pod úhlovým průměrem 1,5 .10-10 radiánů, tj. 3.10-5 obloukové vteřiny. Při stonásobném zvětšení to bude 0,003 obloukových vteřin. Přitom oko vnímá plošku o úhlovém průměru 30 vteřin ještě jako bod. Pokud mám dojem při pozorování prostým okem nebo dalekohledem, že se nám hvězdy jeví jako plošky, má to původ v ohybových jevech v dalekohledu a v oku, v horším případě je to způsobeno horší kvalitou dalekohledu nebo oční vadou.
Odpověď na první otázku bude fyzikálně komplikovanější. Technicky není problémem vyrobit dalekohled s obrovským zvětšením. Problémem je, že v praxi bychom s ním dobře neviděli. Uplatní se totiž dva jevy:
- Neklid ovzduší. V důsledku proudění vzduchu zapříčiněného teplotními rozdíly budeme mít při pozorování dalekohledem s velkým zvětšením dojem, že se díváme na objekt přes rozvlněnou vodní hladinu. To je způsobeno změnou lomu světla při rychlých změnách teploty vzduchové vrstvy, přes níž hledíme. Dalekohled činí tyto jevy tím nápadnější, čím více zvětšuje.
- Ohyb světla. Protože světlo je elektromagnetické vlnění, dochází k jeho ohybu na otvorech a překážkách. Ohyb je tím nápadnější, čím je otvor menší. Při pozorování kruhovým otvorem vznikají kolem bodového obrazu soustředné prstence. Jejich rozměry jsou sice malé, ale jsou tím lépe pozorovatelné, čím je větší zvětšení dalekohledu a menší průměr objektivu. Např. při pozorování dalekohledem o průměru objektivu 20cm se 100-násobným zvětšením, vznikne ohybový kroužek o průměru asi 57 obloukových vteřin ( a další kroužky ještě větší, které však jsou již velmi slabé), což se blíží rozlišovací schopnosti oka.
Závěr je prostý: kvalita dalekohledu (neuvažujeme omezení daná konečnou kvalitou výroby optických členů) je určena především průměrem objektivu.
Pokračování v příštím díle.
Reference
[1] Šulc M., Kosmické rozhledy 1976, No 2, pp. 80-81
[2] Šulc M., 2009, Radiometrické a fotometrické veličiny v astronomii - Díl první
[3] Šulc M., 2009, Radiometrické a fotometrické veličiny v astronomii - Díl druhý
[4] Šulc M., 2009, Radiometrické a fotometrické veličiny v astronomii - Díl třetí