Vypočtěte si hvězdný čas

Ponechme stranou problematiku času slunečního, s poznámkou, že místní střední sluneční čas se ovšem obecně liší od pásmového (v našem případě SEČ) a tím spíše od času letního (u nás SELČ). Připomeňme, že střední sluneční čas je hodinový úhel¹) druhého středního Slunce ²) opravený o 12 hodin.

Hvězdný čas je definován jako hodinový úhel jarního bodu a je výhodné mít tuto definici na paměti, neboť u nezasvěceného může vzniknout dojem, že existují dva (nebo více) fyzikálních časů, což je v newtonovském pojetí časoprostoru nesmysl. Fakt, že tento úhel je běžně vyjadřován v jednotkách časových je sice astronomickým specifikem, ale ničím pozoruhodným. I na analogových hodinách vyjadřujeme úhly sevřené ručičkami se směrem na dvanáctku v jednotkách času, ovšem v jiném přepočtu, neboť ciferník hodin nese nejvyšší hodnotu času 12, nikoliv 24.

Při zdůvodnění rozdílu mezi středním slunečním časem a hvězdným časem (bez úvah o tom, že jeden se počítá "od severu" a druhý "od jihu") vyjdeme z faktu, že tropický rok, (doba mezi dvěma jarními rovnodennostmi), trvá přibližně 365,2422 dne (s přesností lepší než 1 s), což je ovšem počet obrátek Země vůči Slunci. Za jeden tropický rok učiní Země jeden oběh vůči jarnímu bodu. Protože frekvence shodně orientovaných otáčivých pohybů se sčítají, vychází nám, že počet otáček Země vůči jarnímu bodu za tropický rok je udán číslem 366,2422 ³). Poměr těchto dvou čísel je faktor, kterým musíme přepočítat intervaly slunečního času na intervaly času hvězdného nebo naopak. Chceme-li přepočítat interval slunečního času na interval času hvězdného, nutno násobit "sluneční interval" číslem

366,2422/365,2422 = 1,0027379,

při opačném převodu pak "hvězdný interval" číslem

365,2422/366,2422 = 0,99726957   ⁴).

Důvod postupu je zřejmý: poměr délky slunečního dne k délce hvězdného dne musí odpovídat poměru frekvencí. Vynásobíme-li 1 hodinu slunečního času číslem 1,0027379 a převedeme na h, min. a s, obdržíme hodnotu 1 h 00 min. 9,856 s, což je interval hvězdného času příslušný době 1 hodiny slunečního času. Veďme v patrnosti údaj o sekundách, neboť se objeví v dalším výpočtu.

Postup při výpočtu místního hvězdného času na základě znalosti SEČ je dvojí.

1. varianta:

1. Odečtením 1 h od SEČ pro okamžik, který nás zajímá, získáme světový čas SČ - pásmový čas pro nultý (greenwichský) poledník.
2. Přičtením zeměpisné délky stanoviště, vyjádřené v jednotkách času (15⁰ ~ 1 h atd.), získáme místní střední sluneční čas. Východní zeměpisné délky jsou kladná čísla.
3. Takto získanou hodnotu místního středního slunečního času přepočteme na interval hvězdného času buď pomocí tabulek, máme-li je k dispozici, nebo výpočtem podle 3.1.
   1. Převedeme čas vyjádřený v hodinách, minutách a sekundách na čas vyjádřený v hodinách desetinným číslem.Tuto hodnotu násobíme číslem 1,0027379, čímž obdržíme interval hvězdného času. Pak přejdeme opět k vyjádření v hodinách, minutách a sekundách. Tímto postupem jsme se však dopustili systematické chyby - výpočtem jsme ovlivnili i hodnotu zeměpisné délky. Relace 15⁰ ~ 1 h platí nezávisle na druhu času, neboť oba jsou svojí definicí úhly,  stejně jako zeměpisná délka. Tuto chybu je nutno vyloučit tak, že číselnou hodnotu zeměpisné délky stanice, vyjádřenou v hodinách a jejích zlomcích násobíme číslem 9,856 s (viz  výše uvedené upozornění) a součin odečteme.
4. Nalezenou opravenou hodnotu intervalu hvězdného času přičteme k hvězdnému času platícímu pro 0 h SČ téhož dne; tato hodnota je uváděná v Hvězdářské ročence v efemeridách Slunce. Pokud překročíme hodnotu 24 h, je třeba 24 h odečíst.

2. varianta

1. Odečtením 1 h od SEČ pro okamžik, který nás zajímá, získáme světový čas SČ
2. Tento čas, vyjádřený v hodinách, minutách a sekundách, převedeme na čas vyjádřený v hodinách desetinným číslem. Získanou hodnotu násobíme číslem 1,0027379 a převedeme zpět na hodiny, minuty a sekundy intervalu hvězdného času.
3. Nalezenou hodnotu intervalu hvězdného času přičteme k hvězdnému času platícímu pro 0 h SČ téhož dne. Tím získáme hvězdný čas pro daný okamžik v Greenwichi.
4. K takto získané hodnotě připočteme zeměpisnou délku stanice, vyjádřenou v časové míře, tedy hodinách, minutách a sekundách. Poněvadž jsme přičítali zeměpisnou délku až po výpočtu intervalu hvězdného času, není třeba provádět korekce podle bodu 3.1 1. varianty. Překročíme-li po výpočtu dobu 24 h, je třeba 24 h odečíst.

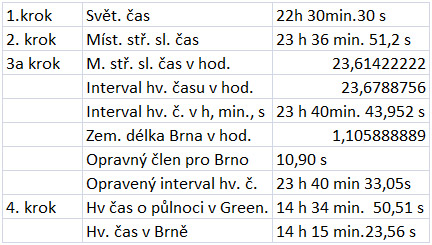
Níže uvedené tabulky demonstrují oba postupy pro poněkud historické datum 1. května 1965, 23 h 30 min. 30 s SEČ v Brně (kopule PF MU) ( v.z.d. 16⁰ 35´18´´0, čili 1h 06min. 21,2 s).

1. varianta

2. varianta

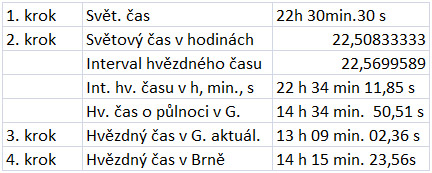
Jak patrno, výsledky v obou variantách se shodují, postup v druhé variantě je však kratší.

Poznámka k obrázku:  Chtěl-li zobrazený pozorovatel určit hvězdný čas, musel ke změřenému hodinovému úhlu hvězdy připočítat její rektascenzi nebo si vhodně natočit stupnici svého přístroje. Pokud to bude chtít čtenář zkoušet podle zobrazeného vzoru, nechť vezme na vědomí, že rektascenze "zadních kol" Velkého vozu je asi 11 h. Kromě toho ciferník přístroje má opačnou orientaci než ciferník hodin a je dělený na 24 hodin. Pro odhad hvězdného času je účelnější použít hvězdu beta v souhvězdí Kassiopey  (je na konci ramene "W", mířícího do souhvězdí Kefea), jejíž rektascenze je asi 0 h 09 min.

---

¹) Hodinový úhel je úhel sevřený rovinou místního poledníku a rovinou určenou světovými póly a objektem na obloze. Měří se od jihu ve směru otáčení oblohy, s časem tedy rovnoměrně narůstá.V daném okamžiku závisí hodinový úhel objektu lineárně na zeměpisné délce stanice.

²) Druhé střední slunce je geometrický bod pohybující se během roku rovnoměrně po světovém rovníku.

³) To ovšem znamená, že hvězdný den (doba mezi kulminacemi jarního bodu) je kratší než den sluneční;  poněvadž obecně velikost intervalu měřeného kratší jednotkou je vyjádřena vyšší číselnou hodnotou, platí to i pro intervaly časové a je tedy interval hvězdného času číselně větší než interval času slunečního.

⁴) Vynásobíme-li tuto hodnotu 24 hodinami hvězdného času, obdržíme rotační periodu Země vyjádřenou v jednotkách slunečního času: 23 h 56 min. 04,09 s.