Teleskopie - díl sedmnáctý (Prodloužení a zkrácení ohniskové vzdálenosti objektivu - Barlowova a Shapleyova čočka)
Je pravděpodobné, že se amatérský astronom, který ve většině případů vlastní jen jeden astronomický dalekohled, bude zajímat o možnosti, jak by jednoduchým vložením dalšího optického členu do systému jeho teleskopu mohl prodloužit nebo zkrátit jeho ohniskovou vzdálenost. Tím lze podstatně rozšířit použitelnost dalekohledu pro různé druhy pozorování nebo fotografování. Barlowova a Shapleyova čočka nejsou jediné, které umožňují prodloužení nebo zkrácení ohniska objektivu. Patří však určitě k nejjednodušším zásahům tohoto druhu, zabezpečují dobrou kvalitu obrazu, nejsou příliš nákladné, proto je považujeme za výhodné.
Barlowova čočka
Barlowova čočka je optický člen, který dovoluje prodloužit ohniskovou vzdálenost objektivu refraktoru nebo reflektoru na dvoj nebo i vícenásobek jeho původní hodnoty. Je to jednoduchá případně dvoj až trojčočková negativní (rozptylná) soustava, kterou umisťujeme do sbíhavého kužele paprsků vycházejících z objektivu, a to nedaleko před jeho ohniskem. Sbíhavé paprsky jsou působením Barlowové čočky rozptýleny tak, že nové ohnisko se vytvoří v určité vzdáleni za původním ohniskem objektivu. Účinek této rozptylky si můžeme znázornit i tak, že objektiv se zdánlivě posune o určitý úsek před jeho původní polohu a vzdálenost mezi ním a novým ohniskem se rovná prodloužené tzv. ekvivalentní ohniskové vzdálenosti. Aby mohla Barlowova čočka splnit uvedenou úlohu, musíme použít negativní čočku s ohniskovou vzdáleností menší, než jakou má vlastní objektiv dalekohledu. Musíme ji umístit před původním ohniskem objektivu tak, aby se její ohnisko na levé straně čočky směrem k okuláru nacházelo až za původním ohniskem objektivu. Důležitá je i skutečnost, že použití uvedeného systému jen v malé míře prodlužuje vzdálenost mezi novým ekvivalentním ohniskem a objektivem, takže je možné použít původní okulárový výtah dalekohledu s krátkým, několikacentimetrovým nástavcem.
výpočet vlastností optického systému objektiv + Barlowova čočka
Především musíme vzít v úvahu, že Barlowova čočka patří k rozptylným (negativním nebo záporným) čočkám, které nemají skutečné ohnisko a nevytvářejí (na rozdíl od spojných čoček) v ohnisku reálný obraz. Svazek světelných paprsků, který přechází rozptylnou čočkou, se za ní rozbíhá na všechny strany. Když tento rozbíhavý svazek prodloužíme přes čočku zpět, jeho paprsky se protnou v jednom bodě, který označujeme jako ohnisko. Vzdálenost tohoto bodu od čočky udává přibližnou ohniskovou vzdálenost této rozptylky, kterou uvádíme vždy se záporným znamínkem mínus (-). Tuto ohniskovou vzdálenost, samozřejmě i se záporným znaménkem, můžeme použít v různých vzorcích při optických výpočtech. O měření ohniskové vzdáleni negativních čoček bude zmínka v dalších odstavcích.

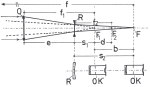
Na obrázku č. 2 nám označuje f1 ohniskovou vzdálenost objektivu O, -f2 ohniskovou vzdálenost Barlowovy čočky a f potom výslednou ekvivalentní ohniskovou vzdálenost celého systému. F1 označuje původní ohnisko (obrazovou rovinu) objektivu O, F2 je rovina zdánlivého ohniska rozptylky R (Barlowovy čočky) a konečně F označuje ekvivalentní ohnisko a obrazovou rovinu vytvořenou celým systémem objektivu O a Barlowovy čočky R. vzdálenosti objektivu O od Barlowovy čočky R je označena písmenem e. Vzdálenost mezi Barlowovou čočkou R a původním ohniskem F1 objektivu O označujeme s1, zatímco úsek mezi rozptylkou R a ekvivalentním ohniskem celé soustavy má označení s2. Z dalších důležitých údajů máme na obrázku znázorněnou vzdálenost původního ohniska objektivu F1 od ohniska rozptylky F2 se symbolem d; konečně úsek mezi původním ohniskem objektivu F1 a ekvivalentním ohniskem F nese označení b.
V našich výpočtech považujeme optické členy soustavy, kterou se zabýváme, za tzv. tenké čočky. To nám dovoluje použít pro výpočty jednoduché rovnice, přičemž výsledky přepočtů jsou dostačující k tomu, aby posloužili amatérskému konstruktérovi při jeho práci.
Základní vzorec, ze kterého budeme vycházet řeší výpočet ohniskové vzdálenosti f dvojčočkového systému (v našem případě se členy O a R) s ohniskovými vzdálenosti f1 a f2; jejich vzájemná vzdálenost je e:
/1/ f = (f1 . f2) / (f1 + f2 - e)
Namísto f1 až e můžeme dosadit s1 (podívejte se na obrázek 2) a rovnici tím zjednodušíme:
/2/ f = (f1 . f2) / (f2 + s1)
Protože ekvivalentní ohnisková vzdálenost f je Anásobkem původní ohniskové vzdálenosti f1 (objektivu O), můžeme napsat:
/3/ f = A . f1 = (f1 . f2) / (f2 + s1)
/4/ A = f2 / (s2 + s1)
Z rovnice 3 vyplývá, že když má být A větší než l a f kladné, potom musí být f2 negativní a větší než s1.
Pro výpočet ohniskové vzdálenosti Barlowovy čočky ve vzdálenosti s1 od ohniska F1, když jsme si zvolili prodloužení původního ohniska dalekohledu o násobek A, nám poslouží rovnice:
/5/ f2 = (A . s1) / (1 - A)
Faktor A určující kolikrát je nová ekvivalentní ohnisková vzdálenost f větší než původní f1 je možné určit i z rovnice:
/6/ A = f / f1 = s2 / s1
Když máme zvolenou výslednou ekvivalentní ohniskovou vzdálenost f pro objektiv s ohniskovou vzdáleností f1 a pro Barlowovu čočku s ohniskovou vzdáleností –f2, můžeme vypočítat, jakou zvolit vzdálenost mezi optickými členy, označenou e, abychom dosáhli požadovaného výsledku:
/7/ e = f1 - f2 - (f1 . f2) / f
Odečtením vzdálenosti e od původní ohniskové vzdálenosti f1 objektivu O zjistíme vzdálenost s1, tedy s1 = f1 – e, kterou však můžeme vypočítat i podle rovnice:
/8/ s1 = f2 (1 - A) / A
Pro vlastní konstrukci a použití Barlowovy čočky má pro nás větší význam hodnota s1 než údaj e, vzhledem na řešení polohy rozptylky R a na její umístění v okulárové části dalekohledu. Vzdálenost mezi Barlowovou čočkou R a ekvivalentním výsledným ohniskem soustavy F je potom určeno rovnicí:
/9/ s2 = f2 (1 - A)
nebo také rovnicí:
/10/ s2 = f2 (f1 - e) / (f1 + f2 - e)
Z uvedené rovnice (9) vyplývá, že při zdvojnásobení ohniskové vzdálenost (A = 2) se bude ekvivalentní ohnisko F nacházet jen o úsek s2 = f2 za Barlowovou čočkou, a proto nedochází k podstatnému prodloužení dalekohledu.
Když je dané f1 a f2 a je určena ekvivalentní ohnisková vzdálenost f, vzdálenost ekvivalentního ohniska F od původního ohniska F1, kterou označujeme b, potom představuje prodloužení celého systému oproti původnímu stavu. Faktor b vypočítáme podle rovnice:
/11/ b = s2 + f2 + d
Pro rovnici (11) si určíme potřebný interval d:
/12/ d = (-f1 . f2) / f
Poloha Barlowovy čočky je v této souvislosti potom určena vzdáleností s1 před původním ohniskem objektivu F1
/13/ s1 = s2 - b
příklady výpočtů
Máme dalekohled s ohniskovou vzdáleností objektivu f1 = 1 000 mm, Barlowovu čočku s ohniskem f2 = -100 mm, kterou umístíme do vzdálenosti e = 950 mm za objektiv, takže ve vzdálenosti s1 = 50 mm před původním ohniskem F1. Podle rovnice (1) potom zjišťujeme:
f = 1000 . (-100) / (1000 - 100 - 950) = 2000mm
Při výše uvedených parametrech soustavy získáme tedy dvojnásobné prodloužení původní ohniskové vzdálenosti. Můžeme však použít i rovnici (2), když si nejprve vypočítáme s1 z rovnice:
s1 = f1 - e = 1000 - 950 = 50mm
f = 1000 . (-100) / (-100 + 50) = 2000mm
V případě, že jsme si pro náš systém zvolili polohu Barlowovy čočky a hledáme, jakou má mít ohniskovou vzdálenost, abychom dosáhli zdvojnásobení původní f1, postupujeme podle rovnice (5):
f2 = (2 . 50) / (1 - 2) = -100mm
Když jsme si pro náš systém zvolili ohniskovou vzdálenost Barlowovy čočky f2 = -100 mm a objektiv O s f1 = 1 000 mm a chceme dosáhnout výsledné ohniskové vzdálenosti f = 2 000 mm (koeficient A = 2), můžeme si vypočítat podle rovnice (7), jaká bude potřebná vzájemná vzdálenost mezi objektivem O a Barlowovou čočkou R:
e = -100 - (1000 . (-100))/2000 = 950mm
Potřebná vzdálenost mezi O a R bude v tomto případě 950 mm.
Podle rovnice (8) vypočítáme, jaká musí být vzdálenost s1 mezi Barlowovou čočkou R a původním ohniskem F1 při zvoleném prodloužení A = 2:
s1 = (-100 . (-1))/2 = 50mm
Tato hodnota platí i pro dalekohled s jinou ohniskovou vzdáleností , protože na ní není závislá.
Rovnici (10) můžeme použít k výpočtu vzdálenosti s2 mezi Barlowovou čočkou R a ekvivalentním ohniskem F, když je známa ohnisková vzdálenost f1 = –1 000 mm a f2 = -100 mm a vzdálenost obou členů O a R:
s2 = -100 . (1000 - 950) / (1000 - 100 -950) = 100mm
Vzdálenost mezi Barlowovou čočkou a ekvivalentním ohniskem F je v tomto případě 100 m.
Důležitým údajem je prodloužení dalekohledu - hodnota b, které vzdáleností nového ekvivalentního ohniska F od původního ohniska F1. K výpočtu můžeme použít rovnici (13):
b = s2 - s1 = 100 - 50 = 50mm
když jsme si již předtím určili s1 a s2 z ohniskové vzdálenosti Barlowovy čočky a z faktoru A (f2 = -100 mm, A = 2) podle rovnic (8) a (9). Máme však možnost postupovat i podle rovnice (11), (12) a (9). Vycházíme zde jen z ohniskových vzdáleností f1, f2 a z ekvivalentní ohniskové vzdálenosti f (f1 = 1 000 mm, f2 = -100 mm, f = 2 000, A = 2):
d = -1000 . (-100) / 2000 = 50mm
s2 = -100 . (1 - 2) = 100mm
b = 100 - 100 + 50 = 50mm
Zvolený systém bude mít tedy ekvivalentní ohnisko o b = 50 mm za původním ohniskem objektivu F1.
použití Barlowovy čočky
1. zvýšení zvětšení dalekohledu
Zvětšení dalekohledu je určeno vzorcem
z = fob / fok
jako podíl ohniskové vzdálenosti objektivu fob a okuláru fok. Při použití stejného okuláru bude zvětšení tolikrát větší, kolikrát prodloužíme ohniskovou vzdálenost objektivu
z = (fob . A) / fok
Pro dosažení větších zvětšení, které můžeme vyjádřit dvojnásobným průměrem objektivu dalekohledu v mm (2Dmm), je často potřeba použít okuláry s velmi krátkou ohniskovou vzdáleností 4 až 6 mm. Tyto optické součástky je těžké získat. Při jejich používání je nutné přiblížit oko do bezprostřední blízkosti oční čočky okuláru. Oční čočka se proto znečisťuje řasami očních víček a dochází k nežádoucímu styku oční rohovky s čočkou okuláru. Malá výstupní pupila v těchto případech často znemožňuje vidět celé zorné pole okuláru.

Abychom získali maximální zvětšení 200x pro dalekohled, který v tomto našem příspěvku používáme jako modelový případ (fob = 1 000 mm, průměr objektivu D = 100 mm), potřebovali bychom okulár s ohniskem 5 mm. dosáhneme toho však i tehdy, když použijeme Barlowovu čočku, která nám prodlouží ohniskovou vzdálenost na dvojnásobek. Potom nám k dosažení maximálního zvětšení stačí okulár s fok = 10 mm.
Každý amatér se snaží, aby měl několik zvětšení pro různé druhy pozorování. Tento problém není nutné řešit celou sérií okulárů. Stačí, když si opatříme např. dva okuláry, jeden s kratším a jeden s delším ohniskem, které potom používáme v kombinaci s Barlowovou čočkou. Posunem Barlowovy čočky směrem od původního ohniska f k objektivu O můžeme měnit faktor A a měnit ohniskovou vzdálenost objektivu (podle f = f1 x A). S kvalitní Barlowovou čočkou a dvěma okuláry můžeme dosáhnout při různých polohách Barlowovy čočky před F1 celé série zvětšení (tabulka 1).
V uvedené tabulce jsou shrnuté výsledky získané s Barlowovou čočkou poměrně velké ohniskové vzdálenosti (- 100 mm), proto je i prodloužení původní délky dalekohledu poměrně velké (sloupec b). Když použijeme rozptylku s poloviční ohniskovou vzdáleností (f2 = -50 mm), prodloužení dalekohledu (b) se při jednotlivých A (2 až 5) sníží též na ½ a bude tedy jen 25, 67, 113 a 160 mm.
2. prodloužení ohniska pro připojení pomocných zařízení k dalekohledu
U amatérských přístrojů se často stává, že konstrukce okulárového výtahu sice dovoluje použít běžné okuláry, ale neumožňuje jeho dostatečné zasunutí, a tak vznikají problémy s používáním pomocných zařízení, jako jsou např. zenitální hranoly, sluneční hranolové systémy a pod., které mají okulár příliš daleko od upínací části, a proto se nedaří získat zaostřený obraz. Barlowova čočka prodlouží ohniskovou vzdálenost na potřebnou délku, takže obrazová rovina objektivu se dostane až k předmětové ohniskové rovině okuláru v přídatném zařízení.

Při výpočtech potřebného prodloužení ohniskové vzdálenosti o b milimetrů budeme vycházet z rovnice (11) nebo z jednoduchého výpočtu b = s2 – s1 a použitím rovnic (8) a (9). V přiložené tabulce č. 2 máme shrnuté hodnoty pro s1, s2 a b pro jednotlivé faktory prodloužení ohniskové vzdálenost (A) od 1,2 po 3,0, odstupňované po 0,2.
Při řešení konkrétního případu postupujeme tak, že ve sloupci b hledáme faktor, který nám dá po vynásobení –f2 (ohniskovou vzdáleností Barlowovy čočky) přibližně hodnotu požadovaného prodloužení ohniskové vzdálenosti v mm. Potom si ve sloupci s1 zjistíme, kolik milimetrů před ohniskem objektivu dalekohledu F1 musíme umístit Barlowovu čočku, a to opět tak, že –f2 vynásobíme příslušným faktorem z tabulky. Abychom např. získali při Barlowovy čočce s f2 = 120 mm prodloužení ohniskové vzdálenosti o 40 mm, použijeme faktor -0,36. Prodloužení bude potom b = -0,36 (-120) = 43,2 mm, což bude pravděpodobně vyhovovat našim požadavkům. Abychom získali toto prodloužení f1 musíme umístit uvedenou Barlowovu čočku do vzdálenosti s1 = -0,44. (-f) = -0,44 x (-120) = 52,8 mm před ohniskem objektivu F1. Ohnisková vzdálenost objektivu dalekohledu O se prodlouží 1,8x (sloupec A, hodnota 1,8). Stejné prodloužení ohniskové vzdálenosti získáme při dodržení uvedených hodnot f2 a s1 při jakémkoli objektivu bez ohledu na jeho ohniskovou vzdálenost. Prodloužení je závislé jen na f2 (na ohniskové vzdálenosti Barlowovy čočky) a na její vzdálenosti s1 před ohniskem dalekohledu F1. Snažíme se používat Barlowovy čočky s takovou ohniskovou vzdáleností, abychom vystačili s prodlužujícím faktorem A menším než 2. Za těchto okolností se potom vady optiky Barlowovy čočky a celého systému projevují jen minimálně a obraz zůstává stejně kvalitní jako bez této pomůcky.
Podle potřeby je samozřejmě možné doplnit tabulku potřebnými hodnotami pro A větší než 3, případně upřesnit faktor b interpolací mezi hodnotami tabulky tak, aby přesně vyhovoval daný požadavek.
3. Barlowova čočka v astrofotogragii
V „pozemské“ fotografii vzdálených objektů, plachých zvířat i všude tam, kde si potřebujeme přiblížit předmět je využití rozptylné čočky před ohniskovou ronivou objektivu na prodloužení jeho ohniskové vzdálenosti už dlouhý čas dobře známé. Tento systém, označovaný názvem „teleobjektiv“, pracuje tedy, na nám už známém, principu Barlowové čočky.
Rozptylná čočka vhodně umístěna v našem dalekohledu může tedy posloužit nejen na zvýšení zvětšení, ale i na to, abychom získali větší obrázky nebeských těles při fotografování přes náš teleskop. Objektiv astronomického dalekohledu spolu s Barlowovou čočkou vytváří tedy astroteleobjektiv s velkou ohniskovou vzdáleností.
Takovéto zařízení je vhodné pro fotografování objektů, které mají dostatečnou jasnost a poskytují i při nízkých světelnostech těchto systémů dostatek světla pro záznam objektu na fotografickém materiálu. Použití Barlowovy čočky přichází v úvahu nejen při snímku Slunce, Měsíce a planet.
Efekt Barlowovy čočky si můžeme přiblížit na příkladu snímku Měsíce. Když budeme fotografovat Měsíc dalekohledem s ohniskovou vzdáleností f1 = 1 000 mm, v jeho ohnisku získáme obrázek této naší oběžnice o průměru 1 000.0,00931 mm, t. j. přibližně 9,3 mm. Na tomto malém obrázku neuvidíme mnoho podrobností ani po jeho dodatečném zvětšení (při kopírování snímku), protože struktura citlivé vrstvy filmu je nemůže pro jejich malé rozměry zobrazit. Při prodloužení ohniskové vzdálenosti f1 na dvoj nebo trojnásobek je už výsledek o dost zajímavější, protože průměr obrázku Měsíce na filmu bude 18,6, případně 27,9 mm. To stejné platí o snímcích Slunce, protože jeho průměr na obloze je stejný jako průměr Měsíce. Zde je vhodné upozornit, že fotografie Měsíce bude při velkých ohniskových vzdálenost (a tedy při velmi nízké světelnosti celého systému 1:20 až 1:40) potřebovat několikasekundové expoziční doby. U Slunce, kde je světla nadbytek, stačí exponovat jen zlomky sekund.
Při výpočtech průměru obrázku Měsíce nebo Slunce můžeme vycházet z rovnice
Dmm = ((f1 . f2) / (f1 + f2 - e)) . 0,00931
Při fotografování planet, pokud máme na snímku rozeznat disk planety a případně větší detaily, musíme použít velké ohniskové vzdálenosti. Průměr disku planety na snímku (Dmm) vypočítáme, když vynásobíme ohniskovou vzdálenost f v milimetrech podle tabulky č. 3.

Faktory pro výpočet průměru obrázků jednotlivých planet, které získáme při fotografování (tabulka 3, sloupec Dmm), platí pro maximální hodnoty, kterých tato tělesa dosahují na obloze při maximálním přiblížení k Zemi (sloupec ø, max.). V opačné podobě mohou být tyto hodnoty podstatně nižší (sloupec ø, min.).
Z uvedených údajů vyplývá, že pokud má mít obraz planety (při maximálním přiblížení k Zemi) v ohniskové rovině alespoň 2 mm, musíme použít ohniskovou vzdálenost objektivu několik metrů (sloupec D2mm). Je samozřejmé, že při takovýchto snímcích velmi záleží na průměru objektivu, který je významným faktorem pro určení expoziční doby, kterou musíme použít i z hlediska možnosti reprodukce jemných detaily.
4. úprava vodícího dalekohledu (pointéru) pomocí Barlowovy čočky
Při delších expozicích snímků oblohy, které si vyžadují fotografie mlhovin, komet, hvězdných polí a podobných objektů se neobejdeme bez tzv. pointéru. Je to dalekohled, kterým kontrolujeme, zda je souběžně uložená fotokamera orientovaná stále na zvolené místo na obloze a zda správně pracuje pohon paralaktické montáže. Pointér dovoluje i vyrovnávat nepřesnosti v poloze komory, které vznikají následkem refrakcí, vlastního pohybu komet a pod. Přesnost vedení fotokomory je závislá na ohniskové vzdálenosti pointéru a na použitém zvětšení. Nároky na přesnost pointace narůstají úměrně s ohniskovou vzdáleností fotoobjektivu. Všeobecné pravidlo říká, že ohnisková vzdálenost pointéru by měla být nejméně taková, jaká je i ohnisková vzdálenost fotokamery, při kratších ohniscích fotoobjektivu i 2 až 4x větší (viz tabulka č. 4).

Když amatérský astronom použije svůj největší objektiv na fotografování a v jeho výbavě se nenachází jiný objektiv s dostatečnou ohniskovou vzdáleností, je možné jako pointér použít i menší dalekohled, který doplní vhodnou Barlowovou čočkou a získá tak přístroj s potřebnou ohniskovou vzdáleností i s potřebným zvětšením.
Protože v tomto případě nevyžadujeme, aby použitý systém měl nejvyšší kvality, můžeme použít prodloužení i na 3 až 4 násobek původní ohniskové vzdálenosti objektivu. Důležité je, aby vytvořený obraz hvězdy použitý pro pointaci dovoloval dostatečně přesné vedení přístroje.
optika pro Barlowovu čočku
Barlowova čočka montovaná v patřičném nástavci je dnes pravidelnou součástí amatérských astronomických dalekohledů předních firem. Je možné zakoupit i samostatný nástavec s optikou přizpůsobený pro použití v okulárových koncovkách různého průměru.
Pokud bychom uvažovali o náhradě originální Barlowovy čočky, přichází zde v úvahu použití zadních (zmenšovacích, negativních) členů běžných teleobjektivů, které bývají často velmi kvalitní a vyhovují pro naše účely. Barlowova čočka by měla být achromatická, tedy složená z negativní čočky z korunového skla a ze spojky z flintového skla. I v případě, že je Barlowova čočka konstruována jako achromat, nemusí dávat v našem dalekohledu uspokojující výsledky, protože někdy je tento člen konstruován tak, aby bezvadně fungoval v určité konkrétní soustavě, s ohledem na její objektiv. Z optických chyb se nejčastěji projevuje chromatická vada (barevné okraje pozorovaných předmětů) a různé deformace obrazu.
Praktické zkoušky ukazují, že pro prodloužení ohniskové vzdálenosti na 1,5 až 2 násobek je možné použít i jednoduchou negativní čočku ploskodutého, nebo vypuklodutého tvaru, kterou obrátíme vydutou částí k okuláru.
Pro malý koeficient prodloužení ohniskové vzdálenosti do A = 2x můžeme použít i negativní brýlovou čočku určenou na korigování krátkozrakosti. Vhodné jsou čočky s optickou silou 10 až 15 dioptrií (-10 až -15 D), které mají ohniskovou vzdálenost -1/10 až -1/15 m (t. j. -100 mm až -66,7 mm). V případě brýlových skel si snadno přepočítáme údaje v dioptriích na ohniskovou vzdálenost podle rovnice
fmm = 1000 / D
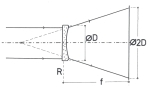
Pokud máme negativní čočku, ať už brýlovou, nebo jinou, a neznáme její ohniskovou vzdálenost, můžeme si tento parametr zjistit následující jednoduchou metodou. Změříme si průměr čočky a na papír si potom narýsujeme kružnici, jejíž průměr bude dvojnásobkem průměru čočky. Papír připevníme na svislou plochu oproti zdroji světla. Čočku přidržíme mezi světelným zdrojem a papírem a pohybujeme s ní, přičemž sledujeme světelný kruh, který vzniká na papírové ploše. V okamžiku, kdy je průměr světelného kruhu shodný s kruhem, který jsme si narýsovali, změříme vzdálenost čočky od papírové plochy. Zjištěná vzdálenost se rovná ohniskové vzdálenosti měřené negativní čočky.
Při použití brýlových čoček bývá potřeba obrousit optický polotovar s průměrem 50 až 60 mm na potřebný menší průměr. Aby měla obroušená čočka potřebné vlastnosti, musí její optická osa i po opracování přecházet přesně jejím středem. Na tento požadavek musíme upozornit v dělení oční optiky.
Amatéři, kteří mají zkušenosti s broušením a leštěním optiky (např. zrcadel) se mohou pokusit o vlastnoruční zhotovení achromatické Barlowovy čočky. Bude se skládat ze záporné složky dvojdutého tvaru a z ploskovypuklé části. Poloměr vydutých ploch rozptylky i poloměr vypuklé plochy pozitivní složky se bude rovnat ½ ohniskové vzdálenosti Barlowovy čočky, kterou chceme zhotovit. Tak např. když má Barlowova čočka mít f = -100 mm, potom poloměr křivosti vydutých ploch bude r = 50 mm, poloměr křivosti vypuklé plochy spojné čočky bude též r = 50 mm.
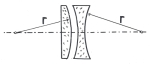
Pro výrobu negativní složky např. korunové sklo BK7 (index lomu n = 1,51633) a pro kladnou čočku flintové sklo SF5 (n = 1,67270), případně jinou vhodnou dvojici skel. Jako materiál je možno použít i roztmelenou achromatickou čočku (spojku), pokud je možné její složky přebrousit do potřebného tvaru. Po vyleštění stmelíme oba členy kanadským balzámem a to tak, že vypuklou plochu spojné čočky vložíme do vyduté části negativní složky.
nástavec pro Barlowovu čočku
Barlowovu čočku, kterou budeme používat při vizuálních pozorováních, upevníme do trubice, která má vnější průměr okuláru, a potom ji zasuneme do objímky pro okulár na konci dalekohledu. Trubici musíme zasunout tak hluboko, aby se negativní čočka dostala do té vzdálenosti před ohniskem objektivu, kterou jsme si vypočítali (údaj s1). Celková délka trubice musí být taková, aby se okulár, který zasuneme do opačného konce trubice, nacházel v ohnisku ekvivalentní ohniskové vzdálenosti F. Její celková délka tedy bude
L = s1 + b = s2
Přesnou délku trubice pro konkrétní okulár musíme potom ještě prodloužit o jeho ohniskovou vzdálenost a (podle typu okuláru) o délku trubičky vlastního okuláru. Obraz zaostřujeme posunem celého nástavce ve směru optické osy přístroje. Vnější konec trubice musí mít samozřejmě takový vnitřní průměr, abychom do něho mohli zasouvat okuláry, které máme k dispozici.
Protože ekvivalentní ohnisková vzdálenost je tím větší, čím je Barlowova čočka dál před ohniskem F1 (směrem k objektivu O), můžeme změnou její polohy měnit i tento faktor, a tím i zvětšení dalekohledu při použití toho stejného okuláru. Současně však musíme počítat s tím, že se bude zvětšovat i vzdálenost b nového ohniska F od F1, a proto musíme úměrně též prodlužovat trubici nástavce. Pokud dobře zvládneme tento problém po stránce mechanické, získáme nástavec s Barlowovou čočkou, který nám dovolí plynule měnit zvětšení dalekohledu ve zvoleném rozpětí.
Při použití Barlowovy čočky pro fotografické účely umístíme negativní čočku do adaptéru (spojovací části), kterým upevňujeme fotokameru k okulárovému výtahu. Vzdálenost Barlowovy čočky od citlivé vrstvy filmu se bude rovnat přesně vzdálenosti s2. Optimální průměr Barlowovy čočky je roven průměru světelného kužele přicházejícího od objektivu, a to v té vzdálenosti, ve které má být čočka umístěna. Jeho průměr si zjistíme vložením průsvitného papíru, nebo matné skleněné desky na patřičné místo. Když bude objektiv obrácený k obloze, objeví se zde světlý kruh, jehož průměr nám udává, jaký má být průměr chystané Barlowovy čočky.
Abychom nebyli zklamaní výsledkem, nezapomeňme na skutečnost, že pro vícenásobné prodloužení ohniskové vzdálenosti potřebujeme kvalitní achromatickou negativní čočku.
zkracování ohniskové vzdálenosti objektivu (Shapleyova čočka)
Ze základní rovnice pro dvojčočkový systém (l) vyplývá, že při spojení dvou kladných (zvětšujících) čoček s ohniskovou vzdáleností f1 a f2 dostáváme optický systém, jehož výsledná ekvivalentní ohnisková vzdálenost f je kratší než původní f1 za předpokladu, že f2 není větší než f1 a pokud je umístíme do vzájemné vzdálenosti menší než f1 + f2. V porovnání s Barlowovou čočkou zde dosáhneme právě opačného účinku.
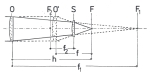
Protože se zkrácením ohniskové vzdálenosti zvyšuje světelnost (D/f) objektivu a optické vady jsou potom výraznější, v úloze Shapleyovy čočky používáme vždy achromatické spojné systémy.
využití Shapleyovy čočky
Oblast využití takto upraveného optického systému dalekohledu je ve skutečnosti jen jediná. Stejně jako její původní amatérský konstruktér Shapley, i dnes ji amatéři používají v těch případech, kdy chtějí adaptovat dlouhoohniskový objektiv (např. F = 1:15) pro fotografování slabých objektů. Dlouhoohniskový objektiv nám dává sice větší obraz fotografovaného objektu, zachytí nám však jen malý úsek oblohy, a takovéto snímky vyžadují velmi dlouhou expoziční dobu. Když zkrátíme ohniskovou vzdálenost objektivu 2x, množství světla vstupující na citlivou vrstvu se zvýší 4x. Množství světla tedy narůstá s druhou mocninou zkrácení ohniskové vzdálenosti. Proto získáme po zkrácení ohniskové vzdálenosti při kratší expozici záznam slabších hvězd, mlhovin, případně komet, než jaké jsme mohli fotografovat před zkrácením ohniska.
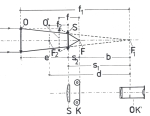
výpočet optických vlastností systému objektiv-Shapleyova čočka
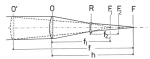
Pro výpočet jednotlivých parametrů soustavy objektiv O plus Shapleyova čočka S, které jsou znázorněny na obrázku č. 8 použijeme ty stejné rovnice, které jsme si uvedli v kapitole o Barlowově čočce.
Jako příklad si zvolíme objektiv s ohniskovou vzdáleností f1 = 1 000 mm a s průměrem 100 mm (D = 100 mm), jehož světelnost je 1:10. Na zkrácení ohniskové vzdálenosti použijeme v úloze Shapleyovy čočky achromatický objektiv s ohniskovou vzdáleností f2 = 175 mm. Chceme dosáhnout změny světelnosti na 1:3,3 ,tedy faktor A, který v tomto případě bude faktorem zkracujícím, se bude rovnat A = 0,33.
Při tomto zkrácení dosáhneme ekvivalentní ohniskové vzdálenosti podle rovnice (3)
f = f1 . A = 1000 . 0,33 = 330mm
Pro výpočet vzdálenosti e, v níž musíme umístit čočku S za objektivem O, abychom dosáhli očekávaný efekt, použijeme rovnici (7)
e = f1 + f2 - (f1 . f2) / f = 1175 - 175000/330 = 644,7mm
Vzdálenost ekvivalentního ohniska zkráceného Shapleyovou čočkou od této čočky S zjistíme podle rovnice (10)
s2 = f2 (f1 - e) / (f1 + f2 - e) = 175 (1000 - 644,7) / (1000 + 175 - 644,7) = 117,3mm
Namísto výpočtu vzdálenosti e mezi čočkami O a S můžeme určit polohu Shapleyovy čočky S před původním ohniskem F1 pro A = 0,33 podle rovnice (8)
s1 = f2 (1 - A) / A = 175 . 0,67 / 0,33 = 355,5mm
Rozdíl mezi polohou původního ohniska F1 a ekvivalentního ohniska po zkrácení F (označený jako úsek b) vypočítáme podle rovnic (11) a (12)
d = (-f1 . f2) / f = (-1000 . 175) / 330 = 5303,3mm b = s2 + f2 + d = 117,3 + 175 - 530,3 = -238mm
Záporné znaménko upozorňuje, že se jedná o zkrácení ohniskové vzdálenosti původního bojektivu, takže poloha ohniska F se nachází o 238 mm blíže k objektivu, než původní ohnisko F1. Údaj o zkrácení ohniskové vzdálenosti můžeme získat i jednoduchým odpočítáním s2 od s1 podle rovnice (13)
b = s2 - s1 = 117,3 - 355,5 = -238,2mm
optika pro Shapleyovu čočku
Využití Shapleyovy čočky je omezené téměř výlučně na úpravu dalekohledu pro fotografické účely. Proto by měla být celá soustava konstruovaná s ohledem na korekci barevné aberace tak, aby vznikající obraz vyhovoval fotografickému materiálu. Refraktorové objektivy určené na vizuální pozorování mají korekci barevné aberace, která pro fotografické účely není dosti vhodná (modrá složka spektra je nejméně korigovaná). Zrcadlový objektiv nemá barevnou vadu, jak ho však spojíme se Shapleyovou čočkou, která bude představovat vizuální achromatický objektiv, barevná vada se zde opět projeví. Nejlepším řešením by tedy byla kombinace zrcadla s fotografickým objektivem ve funkci Shapleyovy čočky. Fotografický objektiv je barevně korigován z hlediska požadavků fotomateriálu.
V případě refraktorového objektivu můžeme opět použít fotoobjektiv jako Shapleyovu čočku, nebo achromatický objektiv z triedru 9×30 (f = 120 mm), nebo 7×50 (f = 175 mm). Zkušenosti s poslední uvedenou kombinací ukazují, že výsledky jsou přijatelné.
Vzhledem na skutečnost, že Shapleyovu čočku vkládáme někdy poměrně daleko před původní ohnisko dalekohledu, je potřeba, způsobem, který jsme už vzpomenuli, zjistit si průměr světelného kužele na tomto místě a přizpůsobit mu i průměr použité Shapleyovy čočky.
původní článek by publikován v Astronomické ročenke (SK) v roce 1999
úprava textu: Petra Váňová, Jihlavská astronomická společnost
Teleskopie: Seriál Jihlavské astronomické společnosti poskytuje cenné rady o konstrukcích astronomických přístrojů v amatérských podmínkách. Autorem seriálu je doc. RNDr. Ivo Zajonc, CSc., autor mnoha publikací nejen o astronomické technice.
Články ze seriálu TELESKOPIE byly v minulých letech postupně uveřejňovány v Astronomické ročenke vydávané Slovenskou ústrednou hvezdárňou v Hurbanove - http://www.suh.sk. Děkujeme vedení tohoto ústavu za souhlas se zveřejněním těchto aktualizovaných příspěvků na webu Jihlavské astronomické společnosti - jiast.cz a České astronomické společnosti astro.cz.

Seriál
- Teleskopie – díl první (Jaký dalekohled je vhodný pro astronoma amatéra?)
- Teleskopie – díl druhý (Zkoušení optického systému astronomických dalekohledů)
- Teleskopie – díl třetí (Jednoduché metody měření a výpočty pro amatérskou konstrukci dalekohledů)
- Teleskopie – díl čtvrtý (Jednoduchý astronomický dalekohled)
- Teleskopie – díl pátý (Triedr v astronomii)
- Teleskopie – díl šestý (Okuláry pro amatérské dalekohledy)
- Teleskopie – díl sedmý (Centrování dalekohledů a nastavení paralaktických montáží)
- Teleskopie - díl osmý (Použití dynametru v astronomické optice)
- Teleskopie - díl devátý (Okno jako astronomická pozorovatelna )
- Teleskopie - díl desátý (Astronom amatér a jeho zrak)
- Teleskopie - díl jedenáctý (Pomůcky pro přímé pozorování Slunce)
- Teleskopie - díl dvanáctý (Projekční metoda pozorování Slunce)
- Teleskopie - díl třináctý (Protuberanční nástavec pro amatérské dalekohledy)
- Teleskopie - díl čtrnáctý (Jednoduché zařízení pro astrografii)
- Teleskopie - díl patnáctý (Fotografujeme astronomickým dalekohledem)
- Teleskopie - díl šestnáctý (Amatérský helioskop)
- Teleskopie - díl sedmnáctý (Prodloužení a zkrácení ohniskové vzdálenosti objektivu - Barlowova a Shapleyova čočka)
- Teleskopie - díl osmnáctý (Optické filtry při amatérských astronomických pozorováních)
- Teleskopie - díl devatenáctý (Jednoduchý způsob měření úhlových vzdáleností na obloze)