Keplerova elipsa ve 4D
Autor: Greg Egan
Matematický fyzik John Carlos Baez v polovině března 2015 na svém blogu zveřejnil zajímavý pohled na problém dvou těles. Děje se odehrávají v tří rozměrném prostoru a čas lze považovat za čtvrtý rozměr. Pokud se použije zvláštní druh času, Moser-Göranssonův čas, tak se hmotné body pohybují po hlavních kružnicích. Pohyb planet kolem Slunce jako pohyb po elipse poprvé popsal před čtyřmi staletími v Praze Johannes Kepler, když proložil pozorováními Marsu od Tychona Braheho elipsu.
Obíhají planety kolem Slunce vždy po kružnici? Ano, ve čtyř rozměrném prostoru.
John Carlos Baez je matematický fyzik, pracuje pro Kalifornskou univerzitu v Riverside a pro singapurské Středisko kvantových technologií. Nedávno na svém blogu, který je součástí projektu Azimuth, zveřejnil zajímavý pohled na problém dvou těles. Pohyb planet kolem Slunce lze zjednodušeně popsat jako problém dvou těles.
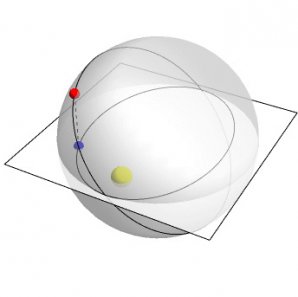
Planety se pohybují v prostoru o 4 rozměrech po kružnicích. A tyto kružnice se při projekci do nám známého prostoru o 3 rozměrech promítají jako elipsy. Následující animaci, která tuto projekci ilustruje, vytvořil Greg Egan.

Rovina na animovaném obrázku představuje 2 rozměry z našeho třírozměrného prostoru, ve kterém žijeme. Svislá souřadnice na animaci představuje čtvrtý rozměr.
Tento čtvrtý rozměr se podobá času, ale není to čas. Na rozdíl od běžného času plyne v obráceném poměru vzdálenosti planety od Slunce; řekněme, že se bude označovat písmenem s, obyčejný čas t, průvodič r.
Platí ds/dt = 1/r.
Podle hlavních protagonistů ho můžeme nazývat Moser-Göranssonův čas. Tento čas plyne ve větší vzdálenosti od centrálního tělesa pomaleji. Animace užívá právě tento druh času. Planeta se v tomto čase pohybuje ve čtyřrozměrném prostoru konstantní rychlostí. Ovšem při projekci do obyčejného třírozměrného prostoru se blíže ke Slunci pohybuje rychleji, než když je dále. Největší rychlost pak má v pericentru, nejmenší v apocentru své dráhy, což je všeobecně známo.
Výše zmíněný popis je jen jiným způsobem, jak přemýšlet o obyčejné Newtonovské fyzice. Pokud je známo, poprvé tento pohled na problém dvou těles, neboli na Keplerovu úlohu, přinesl v roce 1980 německý matematický fyzik Jürgen Moser, který se narodil v pruském Královci, dnes Kaliningrad.
Baezův zápis v jeho blogu vyvolal článek amatérského matematika Jespera Göranssona z 8. března 2015, Symetrie Keplerovy úlohy. Jeho popis problému dvou těles ve 4D totiž umožňuje vzít jakoukoliv eliptickou dráhu, ve výše zmíněném 4D prostoru provést transformaci otočením a získat jinou platnou eliptickou dráhu. Pokud dráha ve výše uvedeném animovaném modelu bude mít vůči svislé, času podobné ose, nulový sklon, tak se do 3D prostoru promítne jako kruhová dráha s nulovou excentricitou. Pokud se její sklon bude zvyšovat, tak se bude zvyšovat excentricita dráhy. Energie dráhy přitom bude konstantní. Kruhové dráhy vedené po hlavních kružnicích 4D koule se budou do našeho třírozměrného prostoru promítat jako elipsy. Poloměr této 4D koule se pro každé konkrétní těleso pochopitelně liší.

Autor: Greg Egan

Animace ukazuje změnu, které dochází při přechodu z obyčejného času na Moser-Göranssonův čas.Nutno říci, že v druhém případě se díváme na kružnici, z jejíhož středu vycházejí rovnoměrně rozložené průvodiče.
Zdá se, že zde popsaný pohled zajímá spoustu čtenářů na celém světě. První den po zveřejnění byl počet čtenářů blogu čtyřnásobný proti normálu a další čtenáři blog komentovali na Google+. Baez se ovšem tady nezastavil a 16. března 2015 vytvořil stránku “Záhady gravitačního problému 2 těles”, kde jsou vidět i souvislosti v mikrosvětě. Znalý čtenář jistě se zájmem prozkoumá zde uvedené odkazy.
Zdroje a doporučené odkazy:
[1] John Baez: Planets in the Fourth Dimmension
[2] Azimuth blog
[3] The Azimuth Project
[4] UC Riverside, Department of Mathematics, John Baez
[5] Center for Quantum Technologies, visiting research professor John Baez
[6] Greg Egan: The Ellipse and the Atom
[7] Jesper Göransson: Symmetries of the Kepler problem
[8] Mysteries of the gravitational 2-body problem
[9] John Baez
[10] Wendy Krieger: The Sky in four dimensions