Zatmění Měsíce a rozdíly v jeho předpovědích

Autor: Fred Espenak
Následující tabulka ukazuje výsledky předpovědí hned z několika zdrojů; časy začátku, středu a konce částečného zatmění jsou udány ve středoevropském čase. Jedná se o naši Hvězdářskou ročenku (HR), Freda Espenaka z NASA Eclipse website (NASA), Institut de Mécanique Céleste et de Calcul des Éphémérides Pařížské observatoře (IMCCE), Her Majesty´s Nautical Almanac Office (HMNAO) a U.S. Naval Observatory (USNO).
|
Zdroj |
Začátek |
Střed |
Konec |
|
HR |
20 54,1 |
21 07,6 |
21 21,0 |
|
NASA |
20 54,1 |
21 07,5 |
21 21,0 |
|
IMCCE |
20 54,0 |
21 07,5 |
21 21,1 |
|
HMNAO |
20 51,7 |
21 07,5 |
21 23,4 |
|
USNO |
20 51,7 |
21 07,5 |
21 23,4 |
Z tabulky je zřejmé, že zatímco okamžiky středu zatmění se prakticky shodují, k poměrně velkým odchylkám dochází u délky trvání celého zatmění. Jasně se zde rýsují dvě skupiny (HR, NASA, IMCCE na jedné straně a HMNAO, USNO na straně druhé), které jsou uvnitř kompatibilní, ale vzájemně se systematicky liší. První skupina odhaduje celkovou délku trvání zatmění na 27 minut, zatímco druhá na téměř 32 minut.
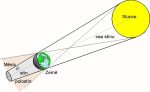
Autor: Jan Vondrák
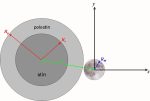
Autor: Jan Vondrák
Skutečný poloměr stínu a polostínu je však závislý též na vlivu zemské atmosféry. Sluneční světlo se totiž při průchodu atmosférou rozptyluje a ohýbá, a tím je způsobeno jednak určité „rozmazání“ hranice stínu (polostínu), jednak zvětšení jeho poloměru. Klasický způsob započtení tohoto vlivu tkví v jednoduchém vynásobení obou poloměrů Rs, Rp, spočítaných dle shora uvedených vzorců, koeficientem 1,02. Po započtení vlivu atmosféry tedy platí Rs = 1,02(π1 -S + πS), Rp = 1,02(π1 +S + πS). Klasický postup tedy zvětšuje poloměr stínu i polostínu ve stejném poměru, relativně o 1/50. Tento způsob stále ještě používají k výpočtům zatmění anglo-americké efemeridy (a tedy v naší tabulce HMNAO a USNO).
Jak ale ukázal známý francouzský astronom, ředitel Pařížské observatoře André Danjon ve své knize z r. 1952 Astronomie générale, není tento způsob zcela správný. V jeho interpretaci je třeba započítat vliv atmosféry tak, že se zvětší pouze poloměr Země o 75 km (tedy relativně zhruba o 1/85 jeho poloměru), což lze jednoduše započítat tak, že se v tomtéž poměru zvětší paralaxa Měsíce. Poloměr Slunce ani jeho paralaxa nejsou přitom zemskou atmosférou nikterak ovlivněny. Spolu se započtením již shora zmíněné redukce z rovníkového na střední poloměr Země pak poloměr stínu/polostínu činí Rs = 1,01πM -S + πS, Rp = 1,01πM +S + πS. Danjonem navržená modifikace tedy v průměru zvětšuje poloměr stínu o 1/73 a polostínu o 1/128. Právě tuto metodu, kterou používá kromě IMCCE i NASA (a byla také použita v knize Canon of Lunar Eclipses autorů Meeus a Mucke, vydané ve Vídni v r. 1983), jsme přijali před mnoha lety též u nás při výpočtech pro Hvězdářskou ročenku.
Rozdíly v tabulce předpovědí zatmění lze tedy jednoznačně přičíst rozdílům v metodě výpočtu vlivu zemské atmosféry; klasický výpočet přitom dává systematicky delší dobu zatmění nežli výpočet podle Danjona. Současně i magnituda zatmění vychází v případě Danjonova postupu poněkud menší (o cca 0,005 v případě stínového a o 0,026 v případě polostínového zatmění) nežli u postupu klasického. V extrémním případě téměř tečného zatmění se dokonce může stát, že klasický postup zatmění předpoví, kdežto Danjonův nikoliv.






